IMO Mérida 2005 (problema 5)
IMO, Mérida, la solución de problemas como deporte
En julio 2005 la comunidad matemática internacional tuvo noticias de México (y la cultura Maya) gracias a que la ciudad de Mérida hospedó la Olimpiada Internacional de Matemáticas, la máxima competencia a la que aspiran llegar los adolescentes que han decidido estudiar matemáticas desde un punto de vista deportivo.
Mérida (y la península de Yucatán) evocan en forma "natural" (por lo menos aquí en México) la cultura Maya y, en particular, Chichen-Itzá (y la pirámide de Kukulkan) --uno de los rastros imposibles de ignorar de un pasado glorioso, de una cultura desaparecida. (La foto es de José Muñoz Porras, a quien le tocó acompañar a la delegación de Taiwan durante la semana del concurso.)

Pero permítaseme comentar sobre el problema 5 del concurso, un problema que le tocó revisar a Jesús Rodríguez Viorato y a quien le prometí trabajar ese problema antes de que él mismo lo comente en una charla del Congreso de la Sociedad Matemática Mexicana la semana del 24 al 28 de octubre de 2005. 
El problema
Sea ABCD un cuadrilátero convexo con lados BC y AD iguales y no paralelos. Sean E y F puntos en los lados BC y AD respectivamente y tales que BE = DF. Las rectas AC y BD se intersectan en P, las rectas BD y EF se intersectan en Q, las rectas EF y AC se intersectan en R. Considere todos los triángulos PRQ a medida que E y F varían. Demostrar que los circuncírculos de esos triángulos tienen otro punto común distinto de P.
Comentarios exploratorios
La primera cosa que se tiene que hacer en problemas de concurso es un acto de fe: lo que se pide demostrar es cierto. En este caso: si se pide demostrar que existe otro punto común a los circuncírculos de los PQR es que sí existe. Y la primera tarea debe ser conjeturar cuál es ese punto, es decir, caracterizarlo tentativamente para después pasar a demostrar que ese es efectivamente el otro punto.
Una buena figura (bien trazada) puede ayudar. De hecho, es necesaria la exploración activa sobre la figura inicial. Una buena actitud para la solución de problemas de concurso es razonar de la siguiente manera: si existe otro punto (y debe existir dado que se está pidiendo su demostración) entonces ese punto debe ser uno de los pertenecientes a la configuración de la figura inicial o bien susceptible de ser caracterizado dentro de ella.
Por ejemplo, un punto de intersección de dos objetos geométricos que puedan ser generados a partir de la figura. (Es como si se dijera "!busca un matemático"! y uno lo que tiene que hacer es buscar en lugares donde acostumbran estar los matemáticos --por ejemplo, en el Instituto de Matemáticas. Me refiero a los lugares en que los podemos encontrar con probabilidad uno.)
Con dos segmentos EF se puede ubicar el segundo punto, llamémosle T, dibujando los circuncírculos correspondientes a los triángulos PQR. Pero todavía falta ver cómo queda caracterizado por los objetos de la figura (u otros auxiliares construidos a partir de aquéllos).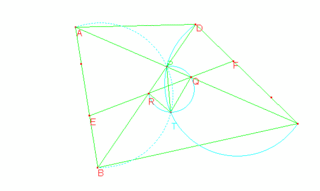
Ahora bien, una vez ubicado T gráficamente, puede uno utilizar de alguna manera el hecho de que (en una traducción de la petición) la configuración PRTQ forma cuadrilátero cíclico (es decir, en el caso de que T fuese el otro punto entonces... si es que vamos a creer en la veracidad de la petición). Y ello nos llevaría a trazar líneas características de los cuadriláteros cíclicos --por ejemplo sus diagonales.
Y como lo que se desea es ubicar T respecto a los objetos geométricos ya conocidos (en la configuración dada en el enunciado), todavía no terminamos. Es necesario más exploración. Con un poco de suerte (y experiencia quizá en problemas parecidos --que no tengo y por eso me llevó mucho más tiempo) se puede llegar a tener la idea --experimentando un poco más con la configuración, acaso por la forma en que está ubicado T en la figura-- que nada perdemos con trazar los circuncírculos de APB y CPD, y es allí donde se logra el descubrimiento: T es el otro punto de intersección de esos circuncírculos. (Y lo mejor es que podemos echar mano de toda la teoría ¡de la geometría del círculo! --y, en particular, de los cuadriláteros cíclicos)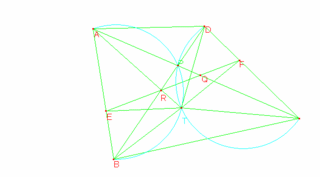
Apuntemos sólo algunas ideas clave de la demostración para no recargar este discurso en modo texto con tanta notación geométrica:
1)Tenemos que buscar los puntos de interfaz entre lo que sabemos (o podemos saber fácilmente a partir de la figura --con los objetos auxiliares ya incorporados--) y lo que queremos saber, es decir, demostrar que PQTR es cíclico. Un ejemplo: el ángulo TPQ es suplementario del TPA, pero el TPA es uno de los ángulos del cuadrilátero cíclico ABTP; el ángulo TPQ es pues un buen punto de interfaz.
2)Es fácil perderse con tantas asociaciones, y posteriores descubrimientos, de ángulos (y sus consecuencias): por ejemplo, en la figura se ven tres isósceles, pero sólo dos son usados. Por eso la brújula debe ser la meta a la que se quiere llegar, en este caso la meta es demostrar PQRT cíclico (y demostrado a partir de ver que dos ángulos característicos son iguales). Y si ya tenemos un ángulo (el QPT) entonces se debe focalizar el correspondiente (el TRQ). Así pues, el llegar al ángulo TRQ debe ser la brújula.
3)El momento inmediatamente anterior a llegar al ángulo TRQ es descubrir que EBRT es cuadrilátero cíclico, a lo cual se llega desde el descubrimiento de que los isósceles BTD y ETF son semejantes. (Con ello se logra ver que los ángulos EBT --que ya sabemos desde el principio que es igual al TPQ-- y TRQ son suplementarios del mismo ángulo ERT, y por lo tanto son iguales.
Digresión didáctica (y de diseño de la instrucción en geometría)
Desde un punto de vista didáctico, el problema 5 de la IMO 2005 (y seguramente todos los otros 5, pero esos todavía no los exploro) es ya un repertorio de habilidades y conocimientos en geometría que se dejan traducir fácilmente a un programa de entrenamiento.
Y los encuentra uno desde el enunciado. Chequen esto: "Mostrar que los circuncírculos..." El mismo término "circuncírculo" apunta a todo una secuencia didáctica: su definición y comprensión, a partir de muchos ejercicios de construcción por ejemplo; el método de construcción de un circuncírculo; sus propiedades; lo mismo para incírculos, excírculos, etc. Y, a partir de ahí, el método de construcción nos llevaría a una inmersión en rectas del triángulo(medianas. mediatrices, bisectrices, etc.) y sus teoremas asociados,...
También en el enunciado, la frase "a medida que EF varía" (que debería entenderse "varía manteniendo sus propiedades") apunta a un entrenamiento en habilidades de lectura de enunciados --sobre todo en la lectura "entre líneas" de enunciados. Y en el reconocimiento del hecho de que, en un enunciado (y en cualquier discurso), no todo está dicho, que ciertos huecos deben ser llenados por el lector.
En la parte de descubrimiento (del otro punto), el conjeturar cuál es el punto T es todo un reto --aunque quizá no tanto para muchos jóvenes que en Mérida resolvieron el problema en alrededor de dos horas. La fase de descubrimiento apunta a un entrenamiento en formas y métodos de exploración y experimentación con configuraciones geométricas. Sobre todo desde un punto de vista dinámico ("a medida que EF varía"). En particular apunta a un entrenamiento en el uso del software de geometría (CBBRI, GSP, Cinderella, ...).
La forma en que yo descubrí el otro punto puede ser ilustrativo. Usé el CABRI (el equivalente francés del Geometer's Sketch Pad). Primero dibujé la configuración de acuerdo al enunciado y después el circuncírculo para PQR. Con ello hice variar EF (tan fácil como mover con el mouse uno de sus extremos). Y observé cómo se movía el circuncírculo.
Sin embargo, eso no me ayudó mucho para descubrir el otro punto. Por eso dibujé, sobre la configuración que ya tenía, otra recta EF para tener dos circuncírculos y ver cuál punto era el que quedaba fijo. De nuevo moví con el mouse uno de los extremos de una recta EF y observé el comportamiento dinámico de la configuración geométrica. Así pude comprobar que efectivamente había otro punto (aparte de P) que se mantenía fijo durante el movimiento de EF. Pero no más.
El comprobar que existía el otro punto me dió cierta seguridad (tuvo un efecto psicológico) pero todavía faltaba caracterizar ese punto fijo T en términos de los objetos de la configuración. Y quizá fue la forma en que se ubicaba T en la figura, con respecto a los restantes objetos, lo que me llevó a más experimentación --en todo caso, con el software de geometría, el experimentar no cuesta casi nada.
Otra idea que me ayudó a lograr la conjetura ya la dije antes pero la repito aquí: la confianza en el axioma (que podríamos llamar axioma de solución de problemas geométricos de olimpiada) de que T debería ser un punto construible a partir de los objetos ya en la configuración.
Esto también tiene un efecto psicológico de descarga de ansiedad, pero también es muy real, y quizá se podría plantear un proyecto de investigación sobre este tipo de enunciados, aparentemente misteriosos pero en los cuales las pistas están ahí mismo en las palabras de esos enunciados --la palabra circuncírculo me revoloteaba en la cabeza...
Así que construí (con el CABRI) los circuncírculos de ABP y CPD y... ¡Oh revelación! Efectivamente, ahí se mostraba claramente que el punto T es la otra intersección de esos circuncírculos.
En resumen, me gustaría recalcar aquí que el uso de un software de geometría maximiza la eficiencia en solución de problemas geométricos. Pero sobre todo la eficiencia en aprendizaje en solución de problemas geométricos --dado que en el concurso sólo se permite el estuche de geometría.
Digamos de paso, y como un reconocimiento asombrado a los jóvenes concursantes, que es una verdadera hazaña de esos muchachos --de los que sí resolvieron el problema 5 en la IMO 2005-- el haber conjeturado el punto T con regla y compás (y el haber demostrado que ese era efectivamente) en el corto espacio de dos o tres horas --dado que cuentan con 4 y media para resolver los tres problemas. (No se descarta la posibilidad de que, con experiencia en problemas parecidos, algunos hayan empezado el problema con "voy a demostrar que el otro punto es la otra intersección..." y se hayan ahorrado el proceso de búsqueda y exploración para lograr la conjetura.
En fin, digamos para finalizar estos comentarios, que la enseñanza o lección que deja la solución de un problema realmente complejo, como lo es el problema 5 de la IMO 2005, es una experiencia de vida (o casi): su recuerdo permanece por largo tiempo en nuestras mentes. Como recuerdo, es decir, de la configuración, de las relaciones entre sus objetos, del plan de demostración, de los pasos intermedios, ...
Y aclaremos que lo que aquí presento es una reconstrucción de una búsqueda que me tomó dos días (y un tercero para redactar esta reconstrucción). Y acaso alguien podría decir "¡qué desperdicio de tiempo"!. Y yo le diría "bueno... cada quien lo pierde de acuerdo a sus propias tendencias y preferencias estéticas..." (¡Qué lata! ahora tendré que ponerme al corriente de la vida privada de los famosos de TELEVISA ¡¿qué travesuras han hecho los de REBELDE?! Pásenme el chisme please!)
Los saluda
JMD en VL



