Conjeturas geométricas dada una configuración
La VI Olimpiada Norestense de Matemáticas (ONM) en Victoria
--por José Muñoz Delgado--
El Evento y su Contexto
En un acto simbólico sin precedentes, la inauguración (el jueves 21 de septiembre) de la VI ONM fue el telón de fondo para anunciar el interés de la Secretaría de Educación de Tamaulipas (SET) y de la Universidad Autónoma de Tamaulipas (UAT) en fortalecer institucionalmente las matemáticas escolares y su enseñanza en el estado a través del proyecto interinstitucional denominado "Aprendiendo Matemáticas para la Vida".
La ONM es un evento que se realiza año con año como un concurso previo a (y de preparación para) el concurso nacional de la Olimpiada Mexicana de Matemáticas (OMM). En la ONM participan Coahuila, Nuevo León Y Tamaulipas, cada uno con 15 adolescentes preseleccionados, y en entrenamiento para su posible participación en el concurso nacional de la OMM.
Las tres delegaciones se hospedaron en el Hotel Holiday Inn Express, la inauguración del evento se realizó en el Centro de Excelencia de la UAT, y el concurso propiamente dicho fue en las instalaciones de la UAM de Ciencias, Educación y Humanidades (UAMCEH) de la UAT.
Los Afanes Matemáticos y su Contexto
Por alguna razón (posiblemente sentimental) los seres humanos somos atraídos a ciertos polos de atracción y alrededor de ellos formamos comunidades (y, se podría decir, tribus). Y siguiendo esa ley humana (demasiado humana) un número considerable
de profesores de matemáticas escolares en Tamaulipas se han reunido alrededor de la Olimpiada de Matemáticas dedicando su tiempo y esfuerzo a la preparación de adolescentes para los concursos, sin más retribución que la mera satisfacción de verlos
elevarse en su nivel de conocimientos y participar en las competencias matemáticas.
En mi caso muy particular, le he dedicado una buena parte de mi tiempo libre a las matemáticas de concurso desde que inició en México la organización de las Olimpiadas de Matemáticas (este año es la 20, así que saquen la calculadora...) con algunos
períodos de incursiones en otros campos (como los dos años y medio --2003 a 2005-- que dediqué a obtener una maestría en comunicación en la universidad más cara de Guadalajara, gracias a PROMEP). Pero este año del 2006 --y desde finales del 2005-- me dediqué a vender mi "atalaya matemática" con el lema "La UAT debe atender al talento matemático adolescente del estado". Y... bueno... contra todos los pronósticos... un servidor y los compañeros profesores que se unieron a mi afán convencimos a
la UAT y la UAT convenció a la SET y el resultado es el proyecto interinstitucional que inició en la inauguración de la ONM.
Creo que estamos en el momento plástico en que la comunidad tamaulipeca de matemáticos, afines y simpatizantes debe unirse al proyecto para que florezca.
Los problemas del concurso
El día del concurso yo andaba con el afán de solicitar (a la Dra.Radmila Bulajich, presidenta del Comité Organizador de la OMM, quien amablemente nos acompañó durante las jornadas del evento) la transferencia de la Delegación de DEGETI hacia la UAT y por eso no tenía planeado estar en el jurado. Pero al llegar ese día del concurso a las instalaciones de la UAMCEH donde tuvo lugar el examen, la delegada actual me convenció de estar presente en el jurado, por lo menos como observador.
Resolver los problemas, decidir los criterios de evaluación para cada uno, revisar los exámenes, discutir sobre el puntaje de los casos no claros y/o controversiales, vaciado concentrador de los puntajes, asignación de los lugares (las medallas) a los concursantes según su desempeño, y la elaboración del informe. Estas fueron las tareas en que estuve involucrado junto con los demás miembros del jurado durante todo el viernes 22 de septiembre --de sol a sol y un poquito más.
Para que el lector pueda formarse una idea del nivel de dificultad de los problemas y el tipo de problemas que los concursantes deben resolver, enseguida los transcribo (la redacción no es mía) y los comento. También transcribo la solución oficial, y redacto una solución alternativa más en el estilo del razonamiento posible de los adolescentes al tratar de resolver esos difíciles problemas.
Problema 1. Demuestre que existen infinitos "m" tales que n^4 + m es un número compuesto para toda "n" entero positivo.
Problema 2. Sean c1 y c2 dos circunferencias que se intersectan en dos puntos A y B. La tangente a c2 por A intersecta a c1 en C y la tangente a c1 por A intersecta a c2 en D. Un rayo que pasa por A, interior al ángulo CAD, intersecta a c1 en M, a c2 en N y al circuncírculo del triángulo ACD en P. Pruebe que AM=NP.
Problema 3. Se tiene una circunferencia de perímetro 210. Se han marcado en la misma 20 puntos, P1, P2, ..., P20, siguiendo el sentido de las manecillas del reloj de modo que el arco que une al punto P1 con P2 tiene longitud 1; el arco que une el punto P2 con el P3 tiene longitud 2; ... y así sucesivamente, el arco que une el punto P20 con el P1 tiene longitud 20. Hallar todos los pares de puntos marcados tales que el segmento que los une es diámetro de la circunferencia.
Comentarios Generales sobre los Problemas
El problema fácil es el 3. Y esto en el sentido de ser más visual y abordable mediante fuerza bruta --basta saber el significado de "diámetro". Sin embargo, habría que decir que el problema 1 es más fácil que el 3, pero en otro sentido: el concursante debe estar convencido de que los enunciados intimidantes en problemas de concurso suelen ser fácilmente "quebrados" traduciendo a un lenguaje menos esotérico.
En el problema 1, esta traducción podría ser "expresar m en función de un entero r, de tal manera que n^4 + f(r) sea factorizable para cualquier r entero positivo". Esta traducción lleva a buscar completar el trinomio cuadrado perfecto, obligar una diferencia de cuadrados y obtener así la m pedida. --el método se podría llamar "de inferencia hacia atrás" y se ilustra en la solución alternativa de este problema mostrada más abajo.
El problema 1, sin embargo, es el fácil de la IMO 1969 y ello demostraría que los jueces de la IMO lo consideraron de nivel internacional. (Ver www.kalva.demon.co.uk/imo/)
El problema realmente difícil es el 2, un problema de geometría del círculo. Y es difícil en dos aspectos. En primer lugar se tiene que ver (o generar --ver solución alternativa más abajo) la idea vinculante, y usarla para construir la solución, lo cual requiere estar familiarizado con las instancias de uso de la geometría del círculo --en particular, ángulos inscritos y semi-inscritos-- para poder establecer las semejanzas entre pares de triángulos que aparecen en la configuración. Y ello suponiendo que el concursante ya domina la terminología geométrica (tangente, circuncírculo, etc.).
Una moraleja que se podría extraer de los problemas 1 (de la IMO 1969) y 2 --y usable para los adolescentes interesados en matemáticas de concurso-- es: "si los puedes resolver en casa es mejor". En casa, es decir, durante la preparación previa al concurso.
Las Soluciones Oficiales
Al igual que en los libros de texto en que la solución de un problema está demasiado comprimida, el ver la solución oficial de los problemas de un examen de olimpiada de matemáticas suele ser frustrante tanto para el adolescente como para sus entrenadores, debido a que resulta, con mucha frecuencia, enigmática –por decir lo menos. No es la excepción el caso de las soluciones de los problemas de la ONM que traían preparadas los miembros del jurado.
Las presento a continuación y les recuerdo a los lectores que, tanto en los libros de texto de matemáticas como en los problemas de concurso, siempre es necesario un trabajo
intelectual adicional para comprender a cabalidad las soluciones.
Solución al problema 1.
n^4 + 4r^4 = (n^2 + 2rn + 2r^2)(n^2 - 2rn + 2r^2). Claramente el primer factor es mayor que 1, el segundo factor es también mayor que 1 para r mayor que 1. Así que podemos tomar m = 4r^2.
Solución al problema 2.
Consideremos, sin pérdida de generalidad, que el rayo es interior al ángulo BAC. Luego, angCMP = angMCA + angCAM = angMAD + angCAM = angCAD. Por otra parte, angCPM = angCAD por subtender el mismo arco. Después, como los triángulos ACD y MCP son semejantes, tenemos MC/AC = MP/AD. Además, angACM = angNAD y angCAM = angADN. Por tanto, los triángulos ACM y DAN son semejantes. Así que AN/AD = MC/AC, y de aquí que MP = AN y AM = NP como se quería. 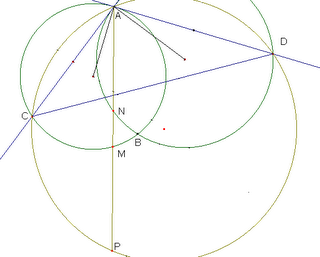
Solución al problema 3.
Buscamos todas las parejas puntos (Pj,Pk), con 0 menor que jmenor que k menor que 21, que cumplan que el segmento que los une sea diámetro. O, equivalentemente, que la longitud del arco que los une sea 105. Pero como la longitud del arco que va de Pj a Pk es
j + (j+1) +...+ (k-1) = (k-1)k/2 - (j-1)j/2,
debemos buscar las parejas que cumplan k-1)k/2 - (j-1)j/2 = 105.
Como (k-1)k/2 - 105 debe ser entero positivo o cero, y para k = 15 es cero, entonces (P1, P15) es una de las parejas buscadas. Las restantes se encuentran dando a k valores mayores a 15 y verificando si el resultado es posible lograrlo con algún j en (j-1)j/2. Las parejas buscadas son (P1, P15), (P6, P16) y (P12, P19).
Soluciones Alternativas y/o Constructivas y Comentarios
Solución constructiva al problema 1
Notemos primero que se desea factorizar n^4 + m. Es decir, queremos n^4 + m = (?)(?). Lo más fácil es completar el trinomio cuadrado perfecto y, en el proceso, tratar de adivinar la forma de m. En primer lugar, notemos que nos conviene hacer m = a^2. Entonces, lo que tenemos que hacer es completar el cuadrado en n^4 + a^2. Veamos:
n^4 + a^2 = n^4 + 2(n^2)a + a^2 - 2(n^2)a = (n^2 + a)^2 - 2(n^2)a.
Ahora bien, para que esta expresión sea factorizable, lo más fácil es verla como diferencia de cuadrados. Por tanto, conviene hacer 2(n^2)a = r^2.
Pero... No. No. Aquí me queda un 2... Así que puedo mejorar mi construcción haciendo 2(n^2)a = (2r)^2. Pero... No. No. Tampoco. La n^2 la puedo dejar fuera pues ya es un cuadrado. Así que es mejor hacer 2a = (2r)^2. Por lo tanto, 2a = 4r^2 o a = 2r^2. Así que a^2 = 4r^4.
(Nótese que de una primera idea de tomar m como un cuadrado perfecto en general, se llegó a una forma de cuadrado perfecto mucho más específica generada por las obligaciones que impone la solución que se pide.)
Después de la fase de búsqueda y exploración de posibilidades anterior (la fase de descubrimiento) ya se puede pasar a la fase de justificación mostrada en la solución oficial. Se tendría, dejando algunos rastros de la fase de búsqueda, algo así como:
n^4 + 4r^4 = (n^2)^2 + (2r^2)^2 + 4n^2(r^2) - 4n^2(r^2) = (n^2 + 2r^2)^2 -(2nr)^2.
Se deja al lector el placer de terminar el argumento.
Solución constructiva al problema 2
La búsqueda de una solución al problema 2 que a continuación se muestra es instructiva de un modo de proceder en solución de problemas de concurso que resulta ser muy eficaz para romper el enigma que representa la pregunta. El enunciado es:
Sean c1 y c2 dos circunferencias que se intersectan en dos puntos A y B. La tangente a c2 por A intersecta a c1 en C y la tangente a c1 por A intersecta a c2 en D. Un rayo que pasa por A, interior al ángulo CAD, intersecta a c1 en M, a c2 en N y al circuncírculo del triángulo ACD en P. Pruebe que AM=NP.
Partamos de la petición. Se pide demostrar AM = NP. Después de una búsqueda mental sobre posibles estrategias generales, uno puede llegar a la conclusión que debería usarse semejanza de triángulos. La estrategia de semejanza es casi infalible en casos como éste en que se da una configuración geométrica con circunferencias traslapadas. Entonces semejanza... Pero de cuáles triángulos... ¡Son muchos! Lo que vamos a hacer enseguida es buscar los triángulos adecuados, es decir, los pares de triángulos semejantes que nos llevarían a la solución.
Lo primero que se tiene que hacer es una buena figura. La ayuda visual es valiosa. En segundo lugar exploremos las posibilidades de triángulos para cada lado de la igualdad:
AM es lado del triángulo AMC (notemos que es el único triángulo en la configuración de que AM es lado). Ahora focalizamos el triángulo AMC buscando ligar sus lados con otros en la configuración: MC es lado del triángulo MCP, y AC es lado del triángulo ACD (y del ACP).
Ahora veamos el otro lado de la ecuación AM = NP. Notemos que aquí, como antes, sólo hay una posibilidad --lo cual nos facilita la tarea. Ahora, como antes, focalizamos el triángulo NPD para buscar ligar sus lados con otros triángulos de la configuración: DN es lado del triángulo DNA, y PD es lado del PDC.
Para facilitar encontrar los pares de triángulos adecuados formemos una tabla de doble entrada:
Lado Triángulo
AM AMC
MC MCP
AC ACD
NP NPD
DN DNA
PD PDC
Con esta tabla y la figura deberíamos llegar (después de un rato de búsqueda) a los pares de triángulos ACD, NPD y AMC, PDC. Para los fines de elaborar una conjetura nos debe bastar con que parezcan semejantes en la figura. Como hay otras semejanzas que pudieran ligar los dos lados de la igualdad a que deseamos llegar, es conveniente explorar si los pares ya encontrados nos llevan a algo sólido.
Si NPD fuese semejante a MCP, se tendría NP/MC = PD/CP (nótese que buscamos que NP y MC estén presentes en la proporción). Y si AMC fuese semejante a DPC, se tendría AM/DP = MC/PC (nótese que ahora buscamos que ligue lo más posible con la anterior).
Entonces, si se dieran esas semejanzas, tendríamos NP/MC = PD/CP = AM/MC y ya llegamos a NP = AM, como se quería. Así que ahora lo que tenemos que hacer es demostrar que realmente se dan esas semejanzas y habremos acabado. Se deja al lector esa tarea. Sólo le damos la sugerencia clave de observar que las tangentes por A a sus respectivas circunferencias son la clave para lograr ver las igualdades de ángulos requeridas para establecer las semejanzas.
Método alternativo para conjeturar las semejanzas adecuadas para el problema 2
De nuevo partimos de la petición de demostrar AM = NP, pero ahora vamos a ir formando razones y proporciones que no alteren la igualdad, pero que al mismo tiempo vayan ligando triángulos en la configuración:
AM = NP
AM/MC = NP/MC (la primera razón ya está, falta resolver la segunda)
AM/MC = NP/MC = (NP/CP)/(MC/CP) (el deno ya está, falta el nume)
(NP/CP) = (NP/PD)/(CP/PD) (y ya está también el nume)
En resumen, tenemos que AM = NP es equivalente, en un sentido algebraico, a AM/MC = [(NP/PD)/(CP/PD)]/(MC/CP). Y ahora buscamos, visualmente ayudados de la figura, cuál razón derecha corresponde a la de la izquierda, de nuevo en una relación visual de semejanza. Es fácil ver que AMC es semejante a DPC y lo que queda es (NP/PD)/(MC/CP), que debe ser la unidad, es decir, debería cumplirse la semejanza entre los triángulos NPD y MCP. ¡EUREKA!
Nota: De nuevo llegamos a la misma conjetura y , de nuevo, falta probar que las semejanzas realmente existen. Hay que decir también que ambos procedimientos son heurísticos, en el sentido de que no aseguran que se llegue una conjetura sólida. Y
también hay que subrayar que en esa búsqueda de semejanzas se podrían seguir callejones sin salida; ante esto lo que se debe hacer es regresar sobre los pasos ya dados y buscar otra ruta.
Conclusión
Hemos querido aquí dar cuenta de la VI Olimpiada del Noreste que tuvo lugar en Cd Victoria Tamaulipas en las instalaciones de la UAMCEH-UAT el viernes 22 de septiembre de 2006. El evento tuvo la importancia añadida de haber sido un acto simbólico que inaugura una época de apoyo gubernamental a las matemáticas escolares en Tamaulipas. Adicionalmente, ha sido un placer comentar sobre los problemas y sus soluciones, así como de un método de conjeturar semejanzas en problemas de geometría y muy útil para problemas de concurso, pues permite focalizar las partes de la configuración gerométrica adecuadas para la solución del problema y evitar así que el adolescente "arroje la toalla" prematuramente ante el caos de líneas y puntos que tiene ante sus ojos sin poder decidirse sobre una ruta prometedora de solución.



