Un problema geométrico elemental
En estos día abrimos en la Universidad (de Tamaulipas) un taller sabatino denominado “Taller de ciencia para jóvenes”. Acudieron a la convocatoria dos profesores de secundaria con 7 de sus alumnos, y un profesor jubilado.
El que esto escribe estuvo a cargo de la sesión con la intención de empezar a desarrollar el tema “Números complejos y Geometría Euclideana”, un tema que me parece muy productivo para la solución de problemas geométricos desde un punto de vista algebraico.
La edad de los asistentes (12 a 15) me hizo dudar, y mejor les pregunté: ¿traen algún problema de geometría que quisieran resolver aquí conmigo? Y su respuesta me hizo dejar en suspenso el tema de complejos y entrar al de congruencia de triángulos, un tema elemental pero que tiene más potencial de lo que uno puede creer para la solución de problemas. Los chicos sacaron su cuaderno y me plantearon el
Problema 1:
En el triángulo ABC, con ángulo recto en B, los puntos E y F están en AC de tal manera que AE=AB y CF=CB. ¿Cuánto mide el ángulo EBF?
Solución:
Decidí aceptar el reto de resolver (ayudar a) este problema elemental de geometría que tiene, sin embargo, sus detalles finos. Empecé con una discusión sobre dibujar la figura y evocar significados teóricos a partir de los datos.
La condición de igualdad de segmentos parece sugerir el uso de congruencia de triángulos. Pero una vez que ve uno más de cerca la figura (sobre todo después de trazar BF y BE) la hipótesis de congruencia debe ser sustituida por la de triángulos isósceles.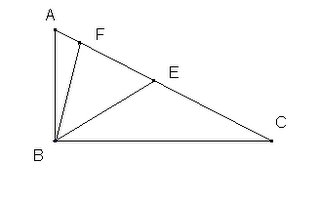
Así pues, es claro que los triángulos ABE y BCF son isósceles. Y una vez que se trae a presencia el concepto de triángulo isósceles, con él viene el de "ángulos en la base iguales."
Hasta aquí, el cognizador tiene la expectativa de que la idea de ángulos iguales en la base le sea de alguna utilidad. Y sí. Porque ello permite la puesta en marcha de la maquinaria algebraica: M=x+y, N=y+z… Y un teoremita elemental que no se había mencionado (la suma de ángulos internos de un triángulo es 180…) llega a salvar toda la situación: M+N+y=180.
Como, además, por dato sabemos que x+y+z=90…un poco de algebra, nos lleva a la respuesta y=45.
Comentemos, para finalizar, que es una experiencia en extremo gratificante para un profesor de matemáticas el tener una audiencia adolescente interesada. Es de hecho una experiencia extraordinaria pues lo común es tener una audiencia cautiva (y lo peor es que el profesor está también cautivo) con todas las implicaciones que pueda tener el adjetivo. Y una de ellas es la indiferencia de la mayoría.
Y si bien es cierto que dentro del aula cotidiana se suelen dar negociaciones para la convivencia pacífica profesor-alumno, también es cierto que la mayoría de las veces esos pactos áulicos no son del todo satisfactorios para las partes --por lo menos para el profesor quien se encuentra tratando de satisfacer dos fuerzas en conflicto: el deber ser de una educación de calidad como respuesta a una sociedad que ingenuamente sigue esperándola del sistema educativo, y la de una realidad educativa que ha acostumbrado a los alumnos a lograr el papel sin ningún esfuerzo de su parte. Ni bueno ni malo, es sólo un hecho de la vida en México. (¿El hecho de que la OCDE nos ubique en último lugar podría en el largo plazo cambiar la situación?)
JMD en VL los saluda... y promete postear más seguido... por lo menos el otro problema que se resolvió en la sesión sabatina del taller...


0 Comments:
Post a Comment
<< Home